
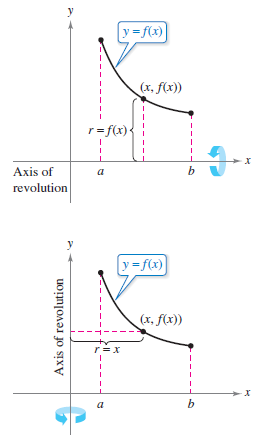
The width of each subinterval is given by the formula Δ θ = ( β − α ) / n, Δ θ = ( β − α ) / n, and the ith partition point θ i θ i is given by the formula θ i = α + i Δ θ. Our first step is to partition the interval into n equal-width subintervals. For polar curves we use the Riemann sum again, but the rectangles are replaced by sectors of a circle.Ĭonsider a curve defined by the function r = f ( θ ), r = f ( θ ), where α ≤ θ ≤ β. Recall that the proof of the Fundamental Theorem of Calculus used the concept of a Riemann sum to approximate the area under a curve by using rectangles. Now we turn our attention to deriving a formula for the area of a region bounded by a polar curve. We have studied the formulas for area under a curve defined in rectangular coordinates and parametrically defined curves. In this section, we study analogous formulas for area and arc length in the polar coordinate system. Similarly, the arc length of this curve is given by L = ∫ a b 1 + ( f ′ ( x ) ) 2 d x. This fact, along with the formula for evaluating this integral, is summarized in the Fundamental Theorem of Calculus. In particular, if we have a function y = f ( x ) y = f ( x ) defined from x = a x = a to x = b x = b where f ( x ) > 0 f ( x ) > 0 on this interval, the area between the curve and the x-axis is given by A = ∫ a b f ( x ) d x. In the rectangular coordinate system, the definite integral provides a way to calculate the area under a curve. 7.4.2 Determine the arc length of a polar curve.7.4.1 Apply the formula for area of a region in polar coordinates.To offer financial support, visit my Patreon page. We are open to collaborations of all types, please contact Andy at for all enquiries. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. Andymath content has a unique approach to presenting mathematics. Visit me on Youtube, Tiktok, Instagram and Facebook. In the future, I hope to add Physics and Linear Algebra content. Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. If you have any requests for additional content, please contact Andy at He will promptly add the content.
#Arc length calculus 2 free
These concepts are important in fields such as physics, engineering, and geometry.” About Ī is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. Other related topics include circular arc length, the circumference of a circle, and the arc length of a curve that is not straight. It is also closely related to the concept of curvature.

It is an advanced topic that builds upon the concepts of limits and derivatives, which are introduced in a first-year calculus course.Īrc length is related to several other concepts in calculus, including integration, limits, and derivatives. Arc length is an important concept in calculus because it allows us to measure and understand the properties of curved objects and shapes.
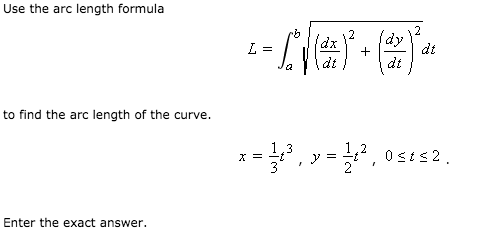
It is a measure of the distance between two points along a curve, rather than a straight line.

In Summary In calculus, arc length refers to the distance along a curved path.


 0 kommentar(er)
0 kommentar(er)
